Deletion in Binary Search Tree (BST)
Difficulty: Medium, Asked-in: Google, Amazon, Qualcomm.
Key takeaway: An excellent problem to learn pointer manipulation in binary trees and problem-solving using both iterative and recursive approaches.
Problem Statement: Given a binary search tree and a key k. Write a program to delete the given key k from the BST and return the updated root node.
Examples
5 5
/ \ delete 2 / \
3 7 ---------> 3 7
/ \ / \ \ / \
2 4 6 8 4 6 8
5 5
/ \ delete 3 / \
3 7 ---------> 4 7
/ \ / \ / / \
2 4 6 8 2 6 8
5 6
/ \ delete 5 / \
3 8 ---------> 3 8
/ \ / \ / \ / \
2 4 6 9 2 4 7 9
\
7Solution idea
To delete a node in a BST, we need to first search for that node. After this, we need to check if there are any nodes present in the left and right subtree of that node. If yes, then we need to appropriately link its subtrees back into the tree somewhere based on the BST property. So, deletion is somewhat trickier than insertion.
Based on the above idea, the strategy for deleting a node from a binary search tree has three cases.
Case 1: Node to be deleted is a node with no children (leaf node): We just delete that node from BST.
Case 2: Node to be deleted is a node with one child: There is one parent and one child node. So we link the child node directly to the parent node and delete that node.
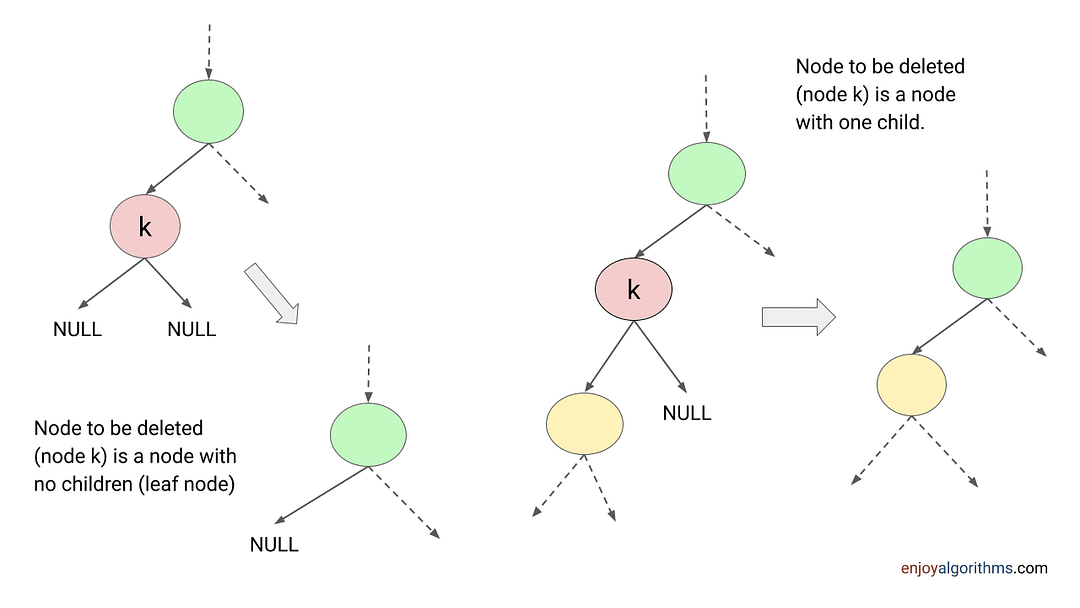
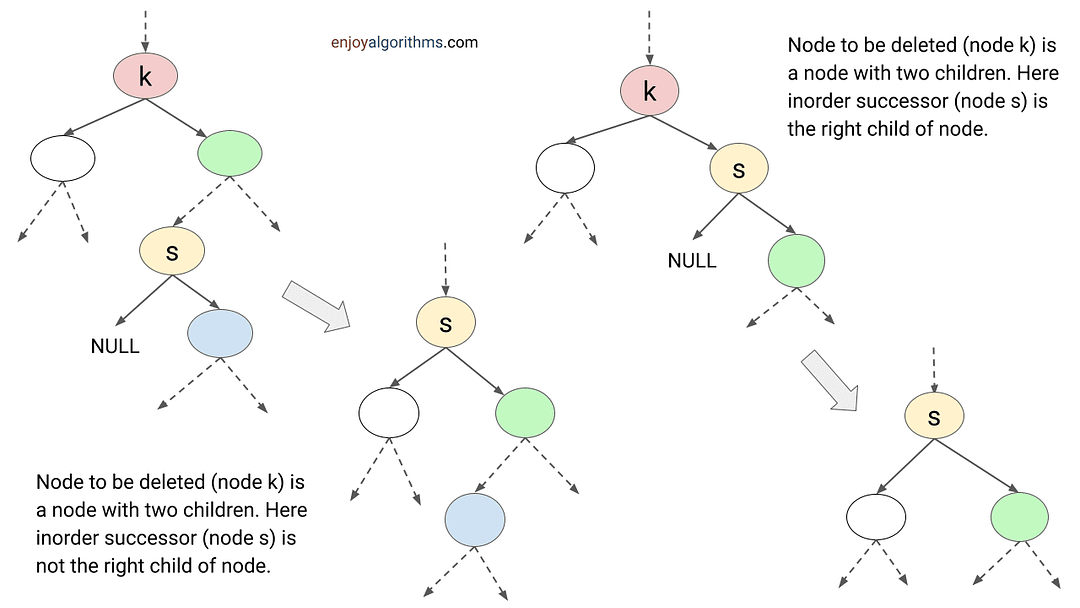
Case 3: Node to be deleted is a node with two children: This one is a little bit tricky because we need to follow three key steps to perform deletion.
- We need to first identify the successor of that node, i.e., a node with a key just greater than the key of the given node to be deleted.
- Then we need to replace the key of the given node with the key of the successor node.
- Delete the successor node.
Because that node has a right child, its successor is the node with the smallest key in its right subtree (leftmost descendant in the right subtree). In other words, key of the successor is the smallest value which is greater than the node key. So this replacement will preserve the BST property because there are no keys between the node's key and the successor’s key.
Now, the critical question is: How can we implement this? We can use both recursive and iterative approaches to search for the key and perform the deletion. Let’s discuss them one by one.
Recursive implementation
Suppose we use a function bstDeleteRecursive(root, k) to delete the node with key k.
Implementation steps
Step 1: If k < root->key, k will be present in the left subtree. So we recursively call the same function for the left subtree to delete that node, i.e., root->left = bstDeleteRecursive(root->left, k).
Step 2: If k > root->key, k will be present in the right subtree. So we recursively call the same function for the right subtree to delete that node, i.e., root->right = bstDeleteRecursive(root->right, k).
Step 3: If k == root->key, we need to delete that node based on the above three cases.
- If the root is a leaf node, return NULL.
- If the root has only the left child, we delete the root node and return its left child.
-
If the root has only the right child, we delete the root node and return its right child.
if (root->left == NULL and root->right == NULL) { free(root) return NULL } else if (root->left == NULL) { BSTNode temp = root->right free(root) return temp } else if (root->right == NULL) { BSTNode temp = root->left free(root) return temp } -
Otherwise, the root has both left and right child. So we find the successor node, set the key of root with the key of the successor, and delete the successor. To find the successor, we call findBSTMin(root->right) to find the node with the minimum key in the right subtree. To delete the successor, we call deleteBSTMin(root->right) to delete the node with the minimum key in the right subtree.
BSTNode successor = findBSTMin(root->right) root->key = successor->key root->right = deleteBSTMin(root->right)
Step 4: Finally, we returns the root node of the modified binary search tree.
Implementation pseudocode
BSTNode bstDeleteRecursive(BSTNode root, int k)
{
if (root == NULL)
return NULL
if (k < root->key)
root->left = bstDeleteRecursive(root->left, k)
else if (k > root->key)
root->right = bstDeleteRecursive(root->right, k)
else
{
if (root->left == NULL and root->right == NULL)
{
free(root)
return NULL
}
else if (root->left == NULL)
{
BSTNode temp = root->right
free(root)
return temp
}
else if (root->right == NULL)
{
BSTNode temp = root->left
free(root)
return temp
}
BSTNode successor = findBSTMin(root->right)
root->key = successor->key
root->right = deleteBSTMin(root->right)
}
return root
}
BSTNode findBSTMin(BSTNode node)
{
while (node->left != NULL)
node = node->left
return node
}
BSTNode deleteBSTMin(BSTNode node)
{
if (node == NULL)
return NULL
if (node->left == NULL)
{
BSTNode temp = node->right
free(node)
return temp
}
node->left = deleteBSTMin(node->left)
return node
}Iterative implementation
We can also implement the above idea iteratively. For this, we iteratively move down the tree to find the node with key k and perform operations based on the above three cases to delete the node.
Implementation steps
Step 1: We first traverse the BST iteratively to find the node with the key to be deleted. For this, we run a loop until either the key is found or the current node becomes NULL. During this process, we also keep track of the parent of the current node.
// Pointer to track the key to be deleted.
BSTNode curr = root
// Pointer to track parent of the key to be deleted.
BSTNode prev = NULL
//Check if key is present in BST.
while (curr != NULL && curr->key != k)
{
prev = curr
if (k < curr->key)
curr = curr->left
else
curr = curr->right
}Step 2: If the key is not found, we simply return the root node. Otherwise, if the current node has only one child or no child, we delete the node by redirecting the parent’s pointer to the current node’s child and deallocating the memory of the current node.
if (curr->left == NULL || curr->right == NULL)
{
// newNode will replace the node to be deleted.
BSTNode newNode
if (curr->left == NULL)
newNode = curr->right
else
newNode = curr->left
// Check if the node to be deleted is the root.
if (prev == NULL)
{
free(curr)
return newNode
}
// Check if the node to be deleted is prev's left or
// right child and then replace this with newNode.
if (curr == prev->left)
prev->left = newNode
else
prev->right = newNode
free(curr)
}Step 4: If the current node has two children, we first find the successor of the current node (the smallest value in the right subtree of the node), copies the value of the successor to the current node, and deletes the successor.
// Pointer to track successor
BSTNode successor
// Pointer to track parent of successor
BSTNode successorParent = NULL
// Now find the successor
// This will be the node with minimum key in right subtree
successor = curr->right
while (successor->left != NULL)
{
successorParent = successor
successor = successor->left
}
// Check if the parent of the successor is the NULL or not.
// If it isn't, then make the left child of its parent equal to the
// successor's right child. Otherwiese, make the right child of the node
// to be deleted equal to the right child of the successor.
if (successorParent != NULL)
successorParent->left = successor->right
else
curr->right = successor->right
curr->key = successor->key
free(successor)Step 5: Finally, we returns the root node of the modified binary search tree after deletion.
Implementation pseudocode
BSTNode deleteBstIterative(BSTNode root, int k)
{
BSTNode curr = root
BSTNode prev = NULL
while (curr != NULL && curr->key != k)
{
prev = curr
if (k < curr->key)
curr = curr->left
else
curr = curr->right
}
// If key is not present in BST
if (curr == NULL)
return root
if (curr->left == NULL || curr->right == NULL)
{
BSTNode newNode
if (curr->left == NULL)
newNode = curr->right
else
newNode = curr->left
if (prev == NULL)
{
free(curr)
return newNode
}
if (curr == prev->left)
prev->left = newNode
else
prev->right = newNode
free(curr)
}
else
{
BSTNode successorParent = NULL
BSTNode successor
successor = curr->right
while (successor->left != NULL)
{
successorParent = successor
successor = successor->left
}
if (successorParent != NULL)
successorParent->left = successor->right
else
curr->right = successor->right
curr->key = successor->key
free(successor)
}
return root
}Time and space complexity analysis
When key k is a node with no child or one child: We need to just search the node with key k and perform some constant time pointer manipulation operation. Suppose the height of the tree is h, then searching takes O(h) time in the worst case because we need to perform one comparison for each level. So in this case, time complexity = O(h) + O(1) = O(h).
When key k is a node with two children: We need to perform three critical operations. Suppose the node to be deleted is present at level m.
- Searching the node will take O(m) time.
- After this, we need to find the successor of the node, which is the leftmost descendant of the right subtree. To find this, we start from the right child of the node. So in the worst case, it will traverse height h - m down the tree. This will take O(h - m) time.
- After this, we need to perform a constant time pointer manipulation operation.
- So overall time complexity = O(m) + O(h -m) + O(1) = O(m + h - m) + O(1) = O(h) + O(1) = O(h).
From the above analysis, we can conclude that deletion in the BST will take O(h) time in the worst case. However, we need to observe one thing: the height (h) of the tree depends on its structure. So there could be two extreme situations:
- Best case: When the tree is balanced, the height will be O(logn). So best time complexity is O(log n).
- Worst case: When we are given a left-skewed or a right-skewed tree, the height of the tree will be O(n). So time complexity in the worst case is O(n).
The space complexity depends on the implementation.
- In iterative implementation, we use constant extra space for storing pointers. So the space complexity of the iterative approach is O(1).
- In recursive implementation, the compiler will use the call stack to simulate the recursion. In the worst case, the call stack size is equal to the height of the tree. So the space complexity of the recursive approach is O(h).
Critical ideas to think!
- When a node has two children, we call two functions separately in the recursive implementation: findBSTMin(root->right) and deleteBSTMin(root->right). Can we optimize this further? Can we keep track of the parent node of the successor so that we can simply remove the successor by doing some pointer manipulation? We know that the successor would always be the leftmost node in the right subtree of the node with key k.
- In the recursive approach, instead of calling deleteBSTMin(root->right), can we call the same function to delete the successor, i.e., bstDeleteRecursive(root->right, successor->key)?
- Instead of using the successor, can we think of implementing the above idea using the predecessor? The predecessor is the node with the maximum key in the left subtree or the node with a key just less than k.
- Can we think of implementing the recursive and iterative approaches in a different way?
- Which one is the better choice: using the successor or the predecessor? Here is an idea: when the right subtree is balanced and has a height less than the height of the left subtree, using the successor will be efficient. Similarly, using the predecessor will be efficient when the left subtree is balanced and has a height less than the height of the right subtree. The critical question is: how do we identify this during the execution process? Can we think of using the successor or predecessor randomly?
If you have any queries or feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!