Dynamic Array Introduction, Implementation and Properties

What is a Dynamic Array?

The drawback of regular arrays is that we cannot adjust their size in the middle of the code execution. In other words, it will fail to add the (n + 1)th element if we allocate an array size equal to n. 

One solution would be to allocate a large array, but this could waste a significant amount of memory. What would be the best solution to this problem? Here is an idea: We can use the idea of dynamic array, where we can increase the array size dynamically as we need it.

How does Dynamic Array Work?

Suppose we start with an array size 1 and double its size whenever we run out of space. This process will allocate a new array of double size, copy the data of the old array to the lower half of the new array, and delete the space used by the old array.

So, the extra overhead in this process is recopying the old data to the new array on each doubling. The critical question is: how many times does an element need to be recopied after n number of insertions? Let's think.

• After the first insertion, we double the array size and copy the first element into the new array. Now array size is 2, and there is one element in the array. So after the second insertion, we need to double the array size to 4 and copy the two elements in the new array.
• Now array size is 4, and there are two elements in the array, so there is no need to resize the array after the 3rd insertion. But after the 4th insertion, the array will be full, and we need to double the array size to 8 and copy the four elements in the new array.

This doubling process continues if we insert the 8th, 16th, 32nd ... elements. In general, after the i number of doubling, the new array size would be 2^i, and there will be 2^(i - 1) elements in the array. So there is no need to resize the array from 2^(i - 1) + 1 to 2^i - 1 insertion. After the 2^i th insertion, the array will get full, and we need to double the array size to 2^(i + 1) and copy the 2^i elements in the new array.

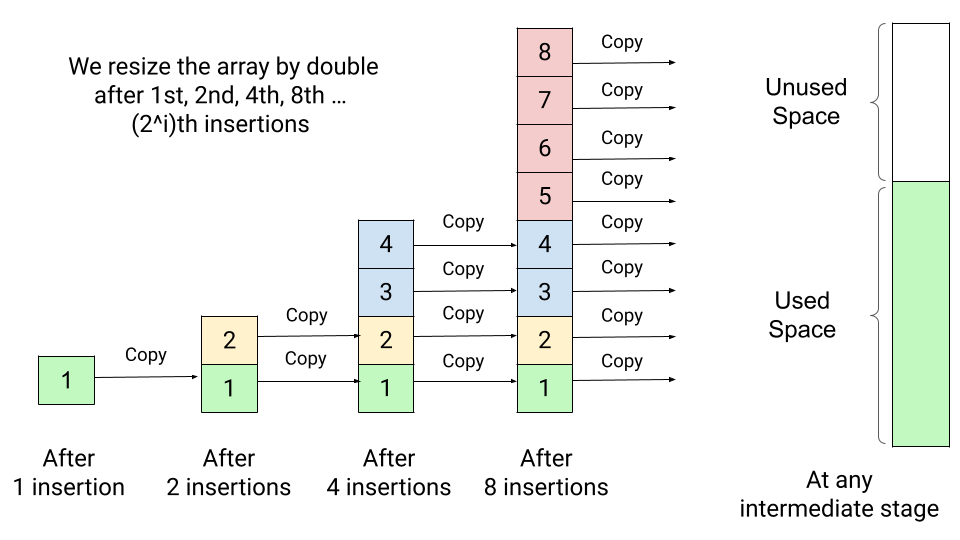
Amortized Analysis of Dynamic Array (Average Case Analysis)

From the above observations, after i number of doubling, if there are n elements in the array, then 2^i = n => i = logn. So after n insertion operations, we need to double the array size logn times. The total number of copy operations after the logn number of doubling = 1 + 2 + 4 + ..... n/4 + n/2 + n.

= n + n/2 + n/4 + ..... + 4 + 2 + 1 

= n (1 + 1/2 + 1/4 + ..... + 4/n + 2/n + 1/n) 

≤ n (1 + 1/2 + 1/4 + ..... + 4/n + 2/n + 1/n + .... till infinity)

≤ n * 1/(1 - 1/2) ≤ 2n

Note: The sum of infinite geometric series 1 + 1/r + 1/r^2 + 1/r^4 + ...till infinity = 1/(1 - r).

For a logn number of insertions (at each doubling point), we need to perform at max 2n copy operations. On the other hand, there is no need to perform copy operations for remaining n - logn insertions. Total copy operation per insertion = 2n / n = 2. So on average, each n element moves only two times, which is constant.

• Expanding the array size by a factor of 2 ensures that inserting n elements takes O(n) time overall. In other words, each insertion will take O(1) time average, almost equivalent to the usual array situation.
• Almost all the insertions will be fast, except for the logn number of insertions, which will trigger array doubling. In other words, the frequency of the best-case scenario is very high (n - logn), and the frequency of the worst-case will be very low (logn). That's why the average time taken per insertion lies closer to the best-case scenario. Explore and think!

Dynamic Array Design and Implementation

For implementing a dynamic array as an abstract data type in C++, Java, or some other programming language, we need to define these things:

• A[]: Pointer to an array.
• currSize: Number of elements in the dynamic array A[]. It is initialized with 0 at the start.
• capacity: Total number of elements that a dynamic array A[] can hold before resizing. It is initialized with 1 at the start.
• Dynamic array constructor: This will get called when we create an object of a dynamic array in our code. It will initialize the value of array pointer A[], currSize and capacity.

Dynamic Array Operations

Now we define and implement dynamic array operations. We can also define other operations based on need.

• void insertAtEnd(int x): Insert an element to the end.
• void reSizeArray(): Increase array capacity by double.
• void shrinkArray(): Decrease array capacity by half.
• void insertAtMiddle(int index, int x): Insert an element to some middle index.
• void deleteAtEnd(): Delete an element from the end.
• void deleteAtMiddle(int index): Delete an element from some middle index.

To work with the oops principles, we declare array pointer A, currSize, and capacity as a private member of the class. This is encapsulation, where we hide the internal details of an object. Similarly, we declare a constructor and operations as public members of the class. This is abstraction where we expose only relevant details to the outside world.

For better abstraction, we can declare reSizeArray() and shrinkArray() methods as private members, because both operations will be used internally by the insertion and deletion methods. So there is no need to provide public access to these methods.

Pseudocode: DynamicArray Class Structure

public class DynamicArray 
{
Private
    int A[]
    int currSize
    int capacity
    void reSizeArray()
    {
        //Implementation code
    }
    
     void shrinkArray()
    {
        // Implementation code
    } 
   
public:
    DynamicArray()
    {
        A = new int[1]
        currSize = 0
        capacity = 1
    }
    void insertAtEnd(int x)
    {
        // Implementation code
    }
  
    void insertAtMiddle(int index, int x)
    {
        // Implementation code
    }

    void deleteAtEnd()
    {
        // Implementation code
    }
  
    void deleteAtMiddle(int index)
    {
        // Implementation code
    }
    
    ...//More dynamic array operations...
}

resizeArray() operation

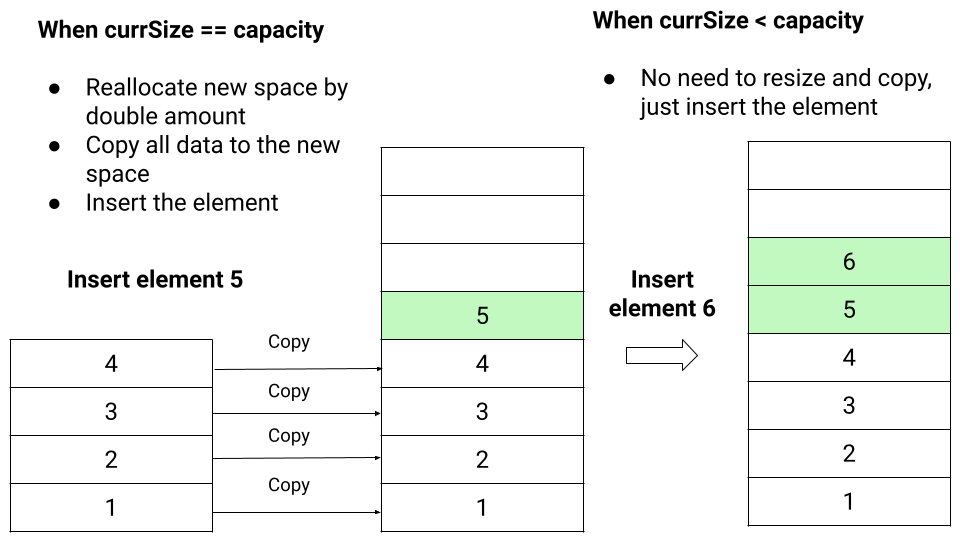
This operation is required when allocated array space gets full with the defined capacity after some sequence of insertion. So we call this method when currSize == capacity during the insertion.

• We double the array capacity and declare a new array temp[] of size 2*capacity.
• We run a loop from i = 0 to capacity - 1 and copy all elements from the original array A[] to the new array temp[].
• We free the space used by A[] and initialize it with temp[].
• Finally, we double the value of capacity.

Pseudocode implementation

void resizeArray()
{
    if (currSize == capacity) 
    {
        int temp[2 * capacity]
        for (int i = 0; i < capacity; i = i + 1)
            temp[i] = A[i]      
        free(A)
        A = temp
        capacity = 2 * capacity
    }
}

insertAtEnd(int x) operation

• If(currSize < capacity), we easily insert the element at A[currSize] and increase currSize by 1.
• Otherwise, array is full of its capacity. So we call resizeArray() operation to double its size, add element x at A[currSize] and increase currSize by 1.

Pseudocode implementation

void insertAtEnd(int x)
{
    if (currSize == capacity)
        resizeArray()
    A[currSize] = x
    currSize = currSize + 1
}

insertAtMiddle(int index, int x) operation

If(currSize == capacity), we resize the array by double and move elements from index to currSize - 1 to one upward. This process will create a space for the new element x. Now we insert the element x at A[index] and increase currSize by 1. Note: If(currSize < capacity), there is no need to resize the array.

Pseudocode implementation

void insertAtMiddle(int index, int x)
{
    if (currSize == capacity)
        reSizeArray()
            
    for (int i = currSize; i > index; i = i - 1)
        A[i] = A[i - 1]
            
    A[index] = x
    currSize = currSize + 1
}

shrinkArray() operation

After some sequence of deletion, currSize of the array may be significantly less in comparison to the current capacity. So dynamic array can also deallocate some of the space if its size drops below a certain threshold, such as 1/4th of the current capacity. This would help in reducing the wastage of extra space.

We perform this operation when currSize == capacity/4 during the deletion.

• We declare a new array temp[] of size capacity/2.
• Now we run a loop from i = 0 to currSize -1 and copy all elements from the original array A[] to the temp[] array.
• We update the new capacity equal to capacity/2 and free space used by A[].
• Finally, we initialize A[] with the new array temp[].

Pseudocode implementation

void shrinkArray()
{
    if (currSize == capacity/4) 
    {
        int temp[capacity/2]
        for (int i = 0; i < currSize; i = i + 1)
            temp[i] = A[i]
        capacity = capacity/2
        free(A)
        A = temp
    }
}  

deleteAtEnd() operation

We need to check the current size of the array. If(currSize == 0), array is empty or there will no element in the array. Otherwise, we remove the element at index currSize - 1 and reduce currSize by 1. During this process, if (currSize == capacity/4), we call the shrinkArray() method to reduce the dynamic array size by half.

Pseudocode implementation

void deleteAtEnd()
{
    if (currSize == 0) 
        print("dynamic array is empty!")
    else    
    {
        A[currSize - 1] = INT_MIN
        currSize = currSize - 1
        if (currSize == capacity/4)
            shrinkArray()
    }
}

deleteAtMiddle(int index) operation

We need to check the current size. If(currSize == 0), array is empty. Otherwise, we move all elements from currSize - 1 to index by 1 downward, set A[currSize - 1] equal to 0, and decrement currSize by 1. During this process, if (currSize == capacity/4), we call shrinkArray() method to reduce the dynamic array size by half.

Pseudocode implementation

void deleteAtMiddle(int index)
{
    if (currSize == 0) 
        print("dynamic array is empty!")
    else    
    {
        for (int i = index; i < currSize - 1; i = i + 1)
            A[i] = A[i + 1]      
        A[currSize - 1] = INT_MIN
        currSize = currSize - 1
        if (currSize == capacity/4)
            shrinkArray()
    }
    
}

Critical concepts to think in dynamic array!

• Analyze and compare time complexities of the above dynamic array operations with the normal array.
• Dynamic array is supplied with standard libraries in many modern programming languages. In C++, it is called a vector, and in Java, it has two implementations: ArrayList and Vector. In Python, the list data type provides dynamic array behavior.
• The growth factor for the dynamic array depends on several things like a time-memory trade-off, algorithms used inside the memory allocator, etc.
• For growth factor k, the average time per insertion operation is k/(k−1), where the maximum number of wasted space will be (k−1)n. Explore the proof behind this concept.
• For the simplicity of analysis, we have used the growth factor k = 2. But if the memory allocator uses a first-fit allocation algorithm, then growth factor values such as k = 2 can cause dynamic array expansion to run out of memory even though a significant amount of memory may still be available.
• There have been several discussions on the ideal values of the growth factor. Some experts suggest the golden ratio value as a growth factor, but library implementation of different programming languages uses different values. Choosing the right growth factor depends on the trade-off between memory usage and resizing frequency. Explore and think!

Enjoy learning, Enjoy algorithms!