Generating all K-combinations

Difficulty: Medium, Asked-in: Amazon, Adobe.

Key takeaway: An excellent problem to learn problem-solving using backtracking and combinatorics. We can use similar ideas to solve other coding questions.

Let’s understand the problem!

Given two numbers n and K and you have to find all possible combinations of K numbers from 1 to n.

Examples

Input: n = 4, K = 2

Output: [ [1 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4] ]

Explanation: We need to select all possible combinations of K numbers from the given n number, which is equal to C(n, K). If n = 4 and K = 2, then value of C(4, 2) = 4!/(2! * 2!) = 6.

Input: n = 5, K = 3

Output: [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5] ].

Explanation: The value of C(5, 3) = 5!/(2! * 3!) = 10.

Important note: Before moving on to the solutions, we recommend trying this problem on paper for atleast 15 or 30 minutes. Enjoy problem-solving!

Discussed solution approaches

Using inclusion and exclusion principle
Using DFS: Fix elements and recur for creating a combination of K numbers

Using inclusion and exclusion principle

Solution idea

If we observe the output pattern of K combinations, there are two possibilities for every number from 1 to n: Either we include the number in the combinations or exclude it from the combination. For example, suppose n = 4 and K = 2. Let's generate combinations of size 2 (refer to the following diagram).

We go left if we include the number and go right if we exclude the number.
At each level, we include or exclude one number at a time.
Each leaf node represents a combination of size 2.

combination tree for finding combinations of K numbers from 1 to n

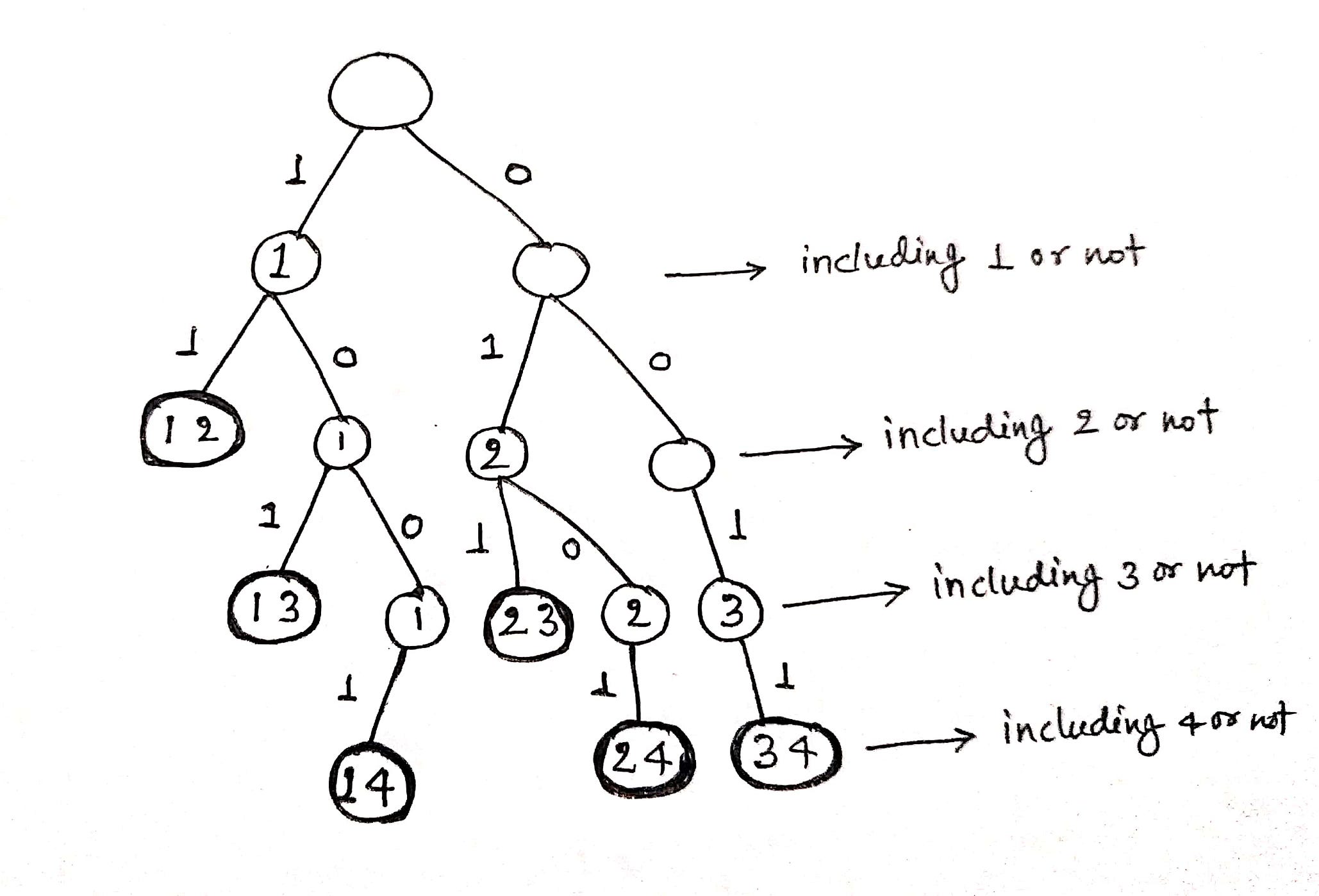
The idea for this approach comes from Pascal's Identity, i.e., C(n, K) = C(n-1, K) + C(n-1, K-1). Here:

C(n, K) is the number of ways to choose K elements from n elements.
C(n-1, K) is the number of ways to choose K elements from n-1 elements (excluding one specific element). In other words, if we exclude the specific element, we are left with n-1 elements and we still need to choose K elements from these n-1 elements. So the total number of combinations after excluding one element = C(n-1, K).
C(n-1, K-1) is the number of ways to choose K-1 elements from n-1 elements (including one specific element). In other words, if we include the specific element in our combination, we now need to choose the remaining K-1 elements from the n-1 elements that are left. So the total number of combinations after including one element = C(n-1, K-1).

To implement this, we consider both cases and recursively create all possible combinations. Suppose we use a function kCombination(output, temp, index, n, i, K), where initial call is kCombination(output, temp, 0, n, 1, K).

Parameters:

output: A 2D vector to store all K combinations.
temp: A temporary vector to store the current combination.
index: The current index in the temp array where the next element will be placed.
n: The upper limit of the range from which elements are selected.
i: The current element being considered for inclusion in the combination.
K: The size of each combination.

Implementation steps

Base case (index == K): When the index reaches K, the current combination stored in temp has K elements. So we add temp to the output vector and return.
Boundary condition (i > n): If the current element i exceeds n, it means there are no more elements to consider, so we return without doing anything further.
Include the current element: We include the current element i in the combination by placing it at the position index in temp. Now we call the same function with the next element (i + 1) and the next index (index + 1) i.e. kCombination(output, temp, index + 1, n, i + 1, K).
Exclude the current element: Now we explore K combinations without including the current element by calling the same function with the next element (i + 1) but without incrementing the index i.e. kCombination(output, temp, index, n, i + 1, K).

Solution code C++

void kCombination(vector<vector<int>>& output, vector<int>& temp, 
                  int index, int n, int i, int K)
{
    if (index == K)
    {
        output.push_back(temp);
        return;
    }   

    if (i > n) 
        return;
    
    // Include the current element
    temp[index] = i;
    kCombination(output, temp, index + 1, n, i + 1, K);
    // Exclude the current element
    kCombination(output, temp, index, n, i + 1, K);
}

vector<vector<int>> findKCombination(int K, int n)
{
    vector<vector<int>> output;
    // Temporary vector to store the combination
    vector<int> temp(K, 0); 
    kCombination(output, temp, 0, n, 1, K);
    return output;
}

Another implementation

This is a slightly different implementation of the above idea.

When temp.size() == K, we add the current combination to the output vector.
We add the current element i to the combination i.e. temp.push_back(i) and call the same function to proceed to the next element (i + 1). This will explore all K combinations including the current element.
Now we backtrack by removing the last element added i.e. temp.pop_back() and call the same function with the next element (i + 1). This will explore all K combinations excluding the current element.

void kCombination(vector<vector<int>>& output, 
                  vector<int>& temp, int i, int n, int K)
{
    if (temp.size() == K)
    {
        output.push_back(temp);
        return;
    }
    
    if (i > n)
        return;
    
    // Include the current element
    temp.push_back(i);
    kCombination(output, temp, i + 1, n, K);
    
    // Exclude the current element
    temp.pop_back();
    kCombination(output, temp, i + 1, n, K);
}

vector<vector<int>> findKCombination(int K, int n)
{
    vector<vector<int>> output;
    // Temporary vector to store the combination
    vector<int> temp;
    kCombination(output, temp, 1, n, K);
    return output;
}

Solution analysis

Here each recursive call will generate two additional recursive calls, and this process continues until the construction of any one of the K combinations or the value of i exceeds n (base cases). On the other side, at each level of the recursion tree, one element is added to the combination. So the maximum depth of the recursion tree is n, and the total number of nodes is proportional to 2^n. Time complexity = O(2^n).

However, this is just a rough estimate, because not all root-to-leaf paths in the recursion tree will have a length of n. The key idea is that during the recursion when the size of the combination reaches K, the algorithm will push the current combination into the output and backtrack from there. This means the algorithm prunes the recursion based on the value of K and effectively explores the C(n, K) valid combinations.

Here output array is part of the problem because we need to return all possible K combinations. So we should not consider output as a part of the space complexity.

We use a temp array of size K to store a combination during the recursive process. So the space complexity for the temp array = O(K).
Here recursion will also use a call stack that is proportional to the max depth of recursion. In this case, the maximum depth is n. So the space complexity for the recursion call stack = O(n).

So overall space complexity = O(K) + O(n) = O(K + n).

Using DFS: Fix elements and recur for creating a combination of K numbers

Solution idea

The idea is to generate a combination tree where we fix each number from 1 to n and recursively build combinations of K numbers. Suppose we have n = 5 and K = 3.

First, we fix the number 1 and recursively generate all unique combinations of size 3 starting with the number 1, such as {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, and {1, 4, 5}.
Next, we fix the number 2 and recursively generate all unique combinations of size 3 starting with the number 2, such as {2, 3, 4}, {2, 3, 5}, and {2, 4, 5}.
Then, we fix the number 3 and recursively generate all unique combinations of size 3 starting with the number 3, such as {3, 4, 5}.
There would be no unique combinations of size 3 starting from 4 and 5.

finding combinations of K numbers from 1 to n example 2

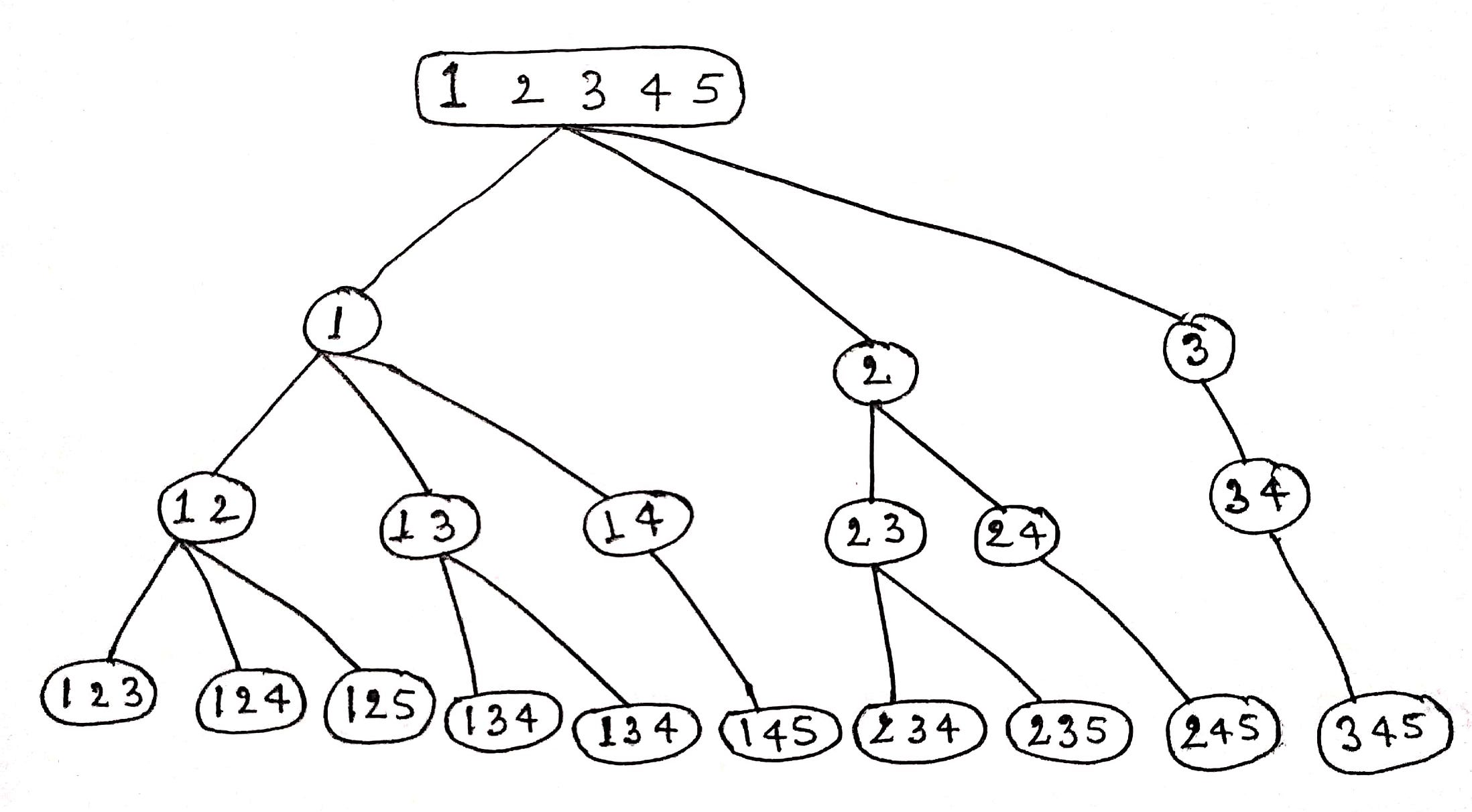
Overall, all K combinations will start from some number. So we first fix the current number and recursively generate all the K combinations starting from that number. After this, we backtrack and move to the next number and do the same thing.

Suppose we are using the function kCombination(output, temp, index, start, end, K) to generate all K combinations, where the initial function call will be kCombination(output, temp, 0, 1, n, K).

Parameters:

output: A 2D vector to store all valid combinations.
temp: A temporary vector to store the current combination.
index: The current position in the temp vector where the next element will be placed.
start: The starting point for the next element in the combination.
end: The upper limit of the range from which elements are selected (equal to n).
K: The final size of each combination.

Implementation steps

Base case (Combination of size K): When index == K, we have generated a new K combination. So we add the current combination in temp to the output and return.
Now we run a loop to iterate over each number from i = start to end and generate all K combinations starting with that number recursively. During this loop, we need to ensure that there are enough elements left to form a complete combination of size K. To ensure this, we add another loop condition end - i + 1 >= K - index.
Inside the loop, For each value of i, we add the element i to the current position (index) in temp. Then we call the same function with the next index (index + 1) and start as i + 1. It will ensure that the next element is selected from the remaining range.

Solution code C++

void kCombination(vector<vector<int>>& output, vector<int>& temp, 
                  int index, int start, int end, int K)
{
    if (index == K)
    {
        output.push_back(temp);
        return;
    }
    
    for (int i = start; i <= end && end - i + 1 >= K - index; i++)
    {
        temp[index] = i;
        kCombination(output, temp, index + 1, i + 1, end, K);
    }
}

vector<vector<int>> findKCombination(int K, int n)
{
    vector<vector<int>> output;
    vector<int> temp(K, 0);
    kCombination(output, temp, 0, 1, n, K);
    return output;
}

Solution analysis

Here we are generating all combinations of size K that can be formed from n elements. So the total number of recursive calls will be approximately nCK (n choose K). So the time complexity of this code is O(nCK).

Critical ideas to think!

What will be the space complexity of the last approach?
In the last approach, why are we checking the condition (end - i + 1 ≥ K - index) inside the loop.
Can we use this idea to solve other similar problems?
Is there a different way to implement the above solutions?
What are the modifications in the algorithm in case of duplicate numbers?

Find all Possible Combinations of K Numbers from 1 to n

Let’s understand the problem!

Examples

Discussed solution approaches

Using inclusion and exclusion principle

Solution idea

Implementation steps

Solution code C++

Another implementation

Solution analysis

Using DFS: Fix elements and recur for creating a combination of K numbers

Solution idea

Implementation steps

Solution code C++

Solution analysis

Critical ideas to think!

Suggested coding problems to practice

More from EnjoyAlgorithms

Self-paced Courses and Blogs

Find all Possible Combinations of K Numbers from 1 to n

Let’s understand the problem!

Examples

Discussed solution approaches

Using inclusion and exclusion principle

Solution idea

Implementation steps

Solution code C++

Another implementation

Solution analysis

U﻿sing DFS: Fix elements and recur for creating a combination of K numbers

Solution idea

Implementation steps

Solution code C++

Solution analysis

Critical ideas to think!

Suggested coding problems to practice

More from EnjoyAlgorithms

Self-paced Courses and Blogs

Using DFS: Fix elements and recur for creating a combination of K numbers