Introduction to Hash Function in Data Structure

In this blog, we discussed the idea of hashing and hash tables. Now we will discuss the design and properties of popular hash functions used in data structures and algorithms.

What is a hash function?

When storing key-value pairs in a hash table, we use a hash function to transform the key into an index in the range of 0 to m-1, where m is the size of the hash table. Here goal of the hash function is to uniformly distribute the keys in this range i.e. each key should have an equal chance of being mapped to any integer between 0 and m-1. This is also known as the assumption of the uniform hashing.

So a good hash function satisfies the assumption of uniform hashing: each key is equally likely to hash to any of the m slots. Unfortunately, this ideal situation is challenging to achieve, making the understanding of hashing interesting!

Now there is another situation. Whatever hash function we choose, there is always a chance of collision i.e. several keys may get mapped into the same slot no matter what hash function we use. Overall, no hash function can map all possible sets of keys without collisions. If the mapping is uniform, the number of keys is n, hash table size is m, then each slot will have approximately n/m keys mapped into it.

Now the critical question is: How do we implement a hash function close to the ideal situation? For this, we need to design a uniform hash function that minimizes the likelihood of collisions. We will discuss collision handling techniques in a separate blog. For now, we are focusing on the design of a hash function.

A basic hash function

If keys are real numbers between 0 and 1, one way to create a hash function is to multiply each key by m and round off to the nearest integer to get an index between 0 and m-1. This hash function can be represented as h(k) = ⌊km⌋. However, this approach has a defect because it gives more weight to the most significant bits of the keys while the least significant bits play no role. Due to this, there are high chances of collision. Think and explore via some examples!

The division method or modular hashing

The most commonly used method for hashing is known as modular hashing, which map a key k into one of the m slots by taking the remainder of k divided by m. This can be represented by the hash function h(k) = k mod m. For example, if table size m = 12 and k = 100, then h(k) = 4. Modular hashing is fast, as it only requires a single division operation. However, it is important to avoid certain values of m or to choose a specific value of m when using this method.

Observation 1: It is not a good idea to choose m as a power of 2. If m = 2^p, the value of k mod m will be the p lowest-order bits of k. This can lead to high collisions if the low-order p-bit of several keys are same. Similarly, if the keys are base-10 numbers and m is 10^k, then the hash function will provide k least significant digits as an output.

Observation 2: To solve the above problem, one solution would be to design a hash function that depends on all the bits of the key. How can we do this? One idea is to choose a prime number for the table size (m). This will ensure that the keys are evenly dispersed between 0 and m - 1. It's often a good idea to choose a prime number that is not too close to an exact power of 2. Think and explore!

Consider a scenario where we need to allocate a hash table to hold 2000 keys (n). To ensure that we only have to examine an average of 3 elements in an unsuccessful search, we can allocate a hash table of size 701 (m). We have 701 because it is a prime number that is near 2000/3, but not close to any power of 2.

Suppose we want to use a hash table to store three-digit telephone area codes (keys) and choose a table size 100 (m). In this case, if the middle digit of the area codes is 0 or 1, the values of k mod m will be concentrated in the range 0 to 20. To disperse the values more evenly, it is better to choose a prime number for table size m that is not close to 100. Similarly, when dealing with IP addresses (which are binary numbers with specific patterns), it's a good idea to use a prime number (not a power of 2) as the table size.

Observation 3: If the size of the table cannot be adjusted easily to be a prime, we can use this hash function: h(k) =(k mod p) mod m, where p is a prime, and p > m (p should be sufficiently larger than m, but it should be sufficiently smaller than the number of all possible keys). 

Observation 4: Sometimes finding a large list of primes is not easy. So another possibility would be this: At random, select two numbers, a and b, such that a < p, b < p, and let h(k) =((ak + b) mod p) mod m. This function is more complicated to compute, but it gives a good average performance for all inputs.

Observation 5: No hash function can be suitable for all inputs. Using primes as described is reasonably safe since most data in practice have no structure related to prime numbers. On the other hand, it can be possible in a particular application that one will want to store the results of some experiments made on integers, all of which are of the form c + kp (here, c is some constant). In such a scenario, all these keys will have the same hash values if m = p. So one idea is to scramble the data one step further, and use a random procedure to select a hash function from a given set of hash functions!

Here is another example! Suppose there are 500 students identified by their social security number, and all possible social security numbers are 1 billion! So it is not a good idea to allocate an array of size 1 billion to store information about them. Instead, we can use the last three digits of the numbers, in which case we need only an array of size 1000. But there may be students with the same last three digits (in fact, with 500 students, the probability of that is relatively high). So in this situation, we can use the last four digits, or the last three digits and the first letter of the student’s name, to minimize duplicates even further. However, using more digits requires a larger-size table and results in a smaller utilization.

A simple Hash Function for strings

Most hash functions assume that keys are a set of natural numbers, i.e., N = {0, 1, 2, 3, ....}. So, if the keys are not natural numbers, we need to find a way to interpret them as natural numbers. For example, in the case of a string, one basic idea is to interpret a string as the sum of the ASCII values of the characters in a string. But this idea can create large chances of collision when large number of strings have same sum of the ASCII values of characters.

int stringHashFunction(String s[], int size, int m) 
{
    int sum = 0
    for(int i = 0; i < size; i = i + 1)
        sum = sum + s[i]
    return sum % m
}

String folding: A better hash function for strings

This function takes a string as input and processes four characters of the string (four bytes data) simultaneously, and interprets each of the four-bytes chunks as a single long integer value. The integer values for the four-byte chunks are added together, and the resulting sum will be converted to the range 0 to m−1 using the modulus operator.

int stringFolding(String s[], int size, int m) 
{
    long sum = 0
    long mul = 1
    for (int i = 0; i < size; i = i + 1) 
    {
        mul = (i % 4 == 0) ? 1 : mul * 256
        sum = sum + s[i] * mul
    }
    return (int)(sum % m)
}

For example, if the string “aaaabbbb” is given, then first four bytes (“aaaa”) will be interpreted as the integer value 1,633,771,873, and the next four bytes (“bbbb”) will be interpreted as the integer value 1,650,614,882. Their sum is 3,284,386,755 (when treated as an unsigned integer). If the table size is 101, then the modulus operator will hash this key to slot 75 in the table.

The Mid-Square Method

The mid-square method is a good hash function for the integer key. It squares the key value, takes out the middle r bits of the result and provides a hash value in the range 0 to 2^r - 1. It will work well because most or all bits of the key have contributed to the result.

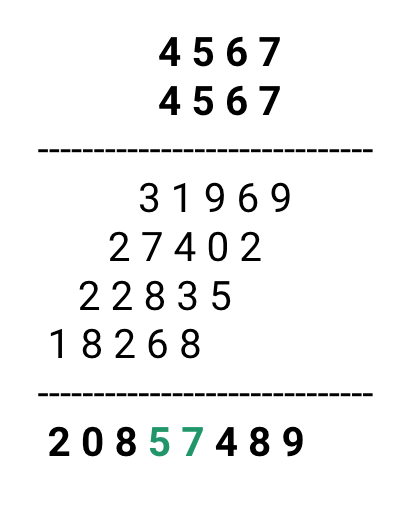
For example, consider records whose keys are 4-digit numbers of base 10, and the goal is to hash these keys to a table of size 100 i.e. a range of 0 to 99. This range is equivalent to two digits in base 10, so r = 2. If the input is number 4567, squaring yields an 8-digit number, 20857489.

The middle two digits of this result are 5 and 7. If we observe, all digits of the original key (equivalently, all bits when the number is in binary) contribute to the middle two digits after taking the square. So the final result will not be dominated by the distribution of the lower-order digit or the higher-order digit of the original key.

The Multiplication Method

The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0< A < 1 and extract the fractional part of kA. Then, we multiply this value by m and take the floor of the result. In short, the hash function is h(k) = ⌊m(kA mod 1)⌋, where “kA mod 1” means the fractional part of kA, that is, kA - ⌊kA⌋. An advantage of the multiplication method is that the value of m is not critical. We can choose it as a power of 2, i.e., m = 2^p for some integer p.

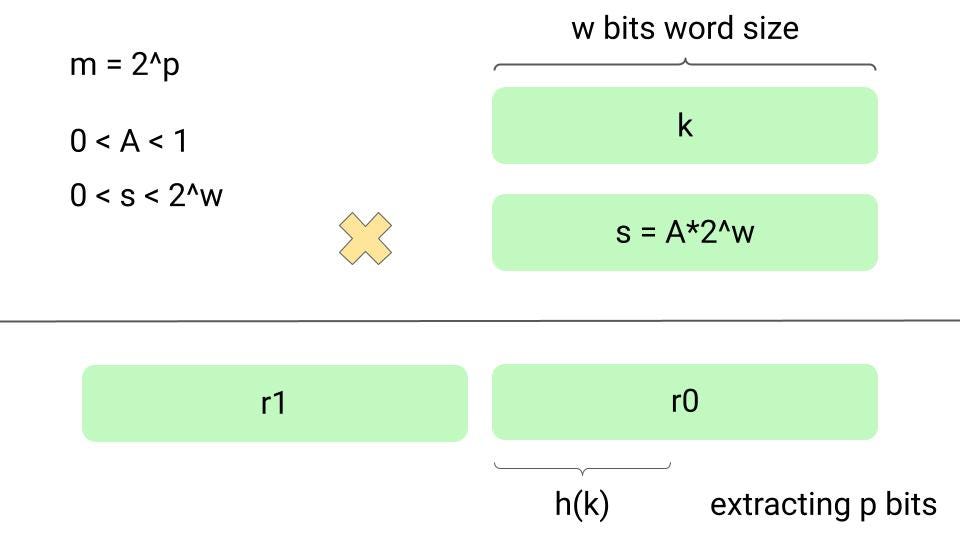
Suppose that the machine's word size is w bits and key k fits into a single word. We restrict A to be a fraction of the form s/2^w, where s is an integer in the range 0 < s < 2^w.

We first multiply k by the w-bit integer s = A*2^w. The result is a 2w-bit value r1*2^w + r0, where r1 is the high-order word of the product and r0 is the low-order word of the product. The desired p-bit hash value consists of the p most significant bits of r0. Although this method works with any value of the constant A, it works better with some values than others. The optimal choice depends on the characteristics of the data being hashed. Think!

Special note around hash functions

• Uniformity and randomness are the essences of hashing. In other words, hash functions should transform a set of keys uniformly to a set of random locations in the range 0 to m - 1.
• A good hash function generates the hash values from keys in a way independent of any patterns that might exist in the data. For example, the modular hashing frequently gives good results, assuming that we choose m as a prime number that is unrelated to any patterns in the distribution of keys.
• Of course, the same hash function must be used for all accesses to the same table. In many cases, however, there is a need for many independent tables that are created and destroyed frequently. In those cases, we can use a different hash function every time, when we create a different table.
• Information about the distribution of keys can help us to design an efficient hash function. For example, suppose the keys are strings representing the name of the person, then closely related names, such as "Mohan", "Sohan", "Rohan" may often occur. Here a good hash function should minimize the chance that such names hash to the same slot. In other words, some applications of hash functions might require stronger properties than the condition of the simple uniform hashing.

Enjoy learning, Enjoy algorithms!