Trie: An Efficient Data Structure for String Processing

Trie is a type of search tree. It is a famous data structure used to store and process data, especially strings. The word trie comes from retrieval as a trie can retrieve all the words with a given prefix.

Consider this problem statement

Suppose, we want to implement a dictionary of words and perform the following operations:

1. Adding a word
2. Searching a word
3. Removing a word

We can do this easily using a hashmap. The average time complexity of insertion, deletion, and searching in a hashmap will be O(wordLength), as we would need to calculate the hashcode for it, which would require the traversal of the whole word. In a trie, the time complexity of the above operations is also O(Word Length) always (explained later), which is slightly faster than hashmaps. 

Are we using tries for this slight improvement? The answer is no! The main strength of tries lies in its ability to operate the word’s prefix. Suppose the problem statement is that given a string, we need to find all the words in the dictionary. If we have used a hashmap to store the words, we need to iterate through all the words in the hashmap and check if their prefix is the same. This takes O(numWords * maxLength) time, where numWords is the number of words in the dictionary, and maxLength is the maximum length of a word in the dictionary. We will see that this is done efficiently in a trie.

Structure of trie data structure

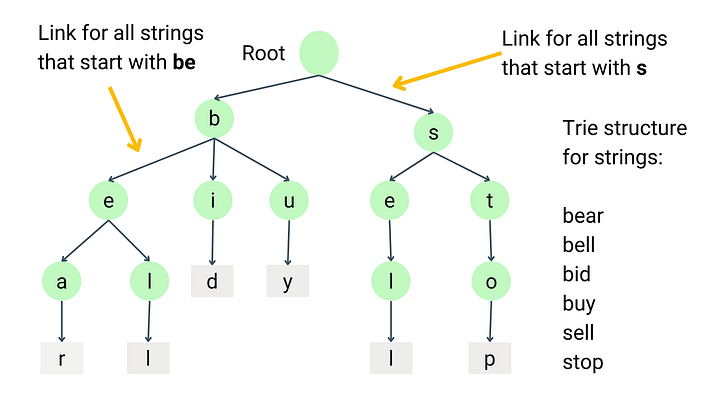
The trie is a tree where each node represents a prefix or end of a word (the path traced from the root to that node). Suppose k is the count of all possible unique characters in an alphabet, then each node in the trie stores:

• A bit indicating if this node is an end of a word or not.
• Pointer or reference to child nodes: This is an array of pointers of size k, where one pointer for each possible character in the alphabet. Suppose, we have only lowercase letters in the string, then there are only 26 possible unique characters from ‘a’ to ‘z’. So k = 26 and the maximum number of children any node can have is 26.

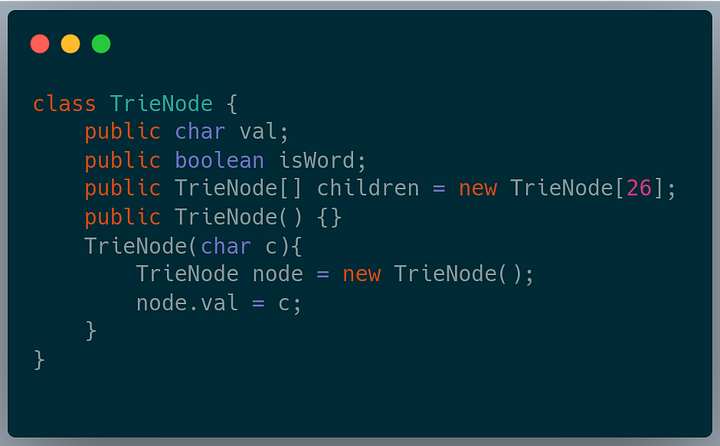
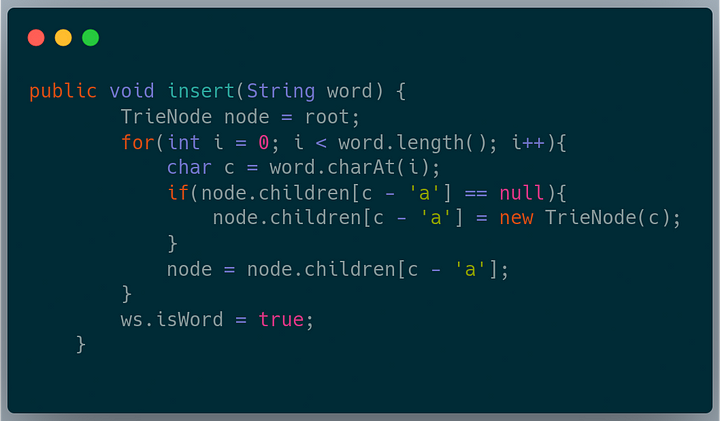
Following is the trie node class

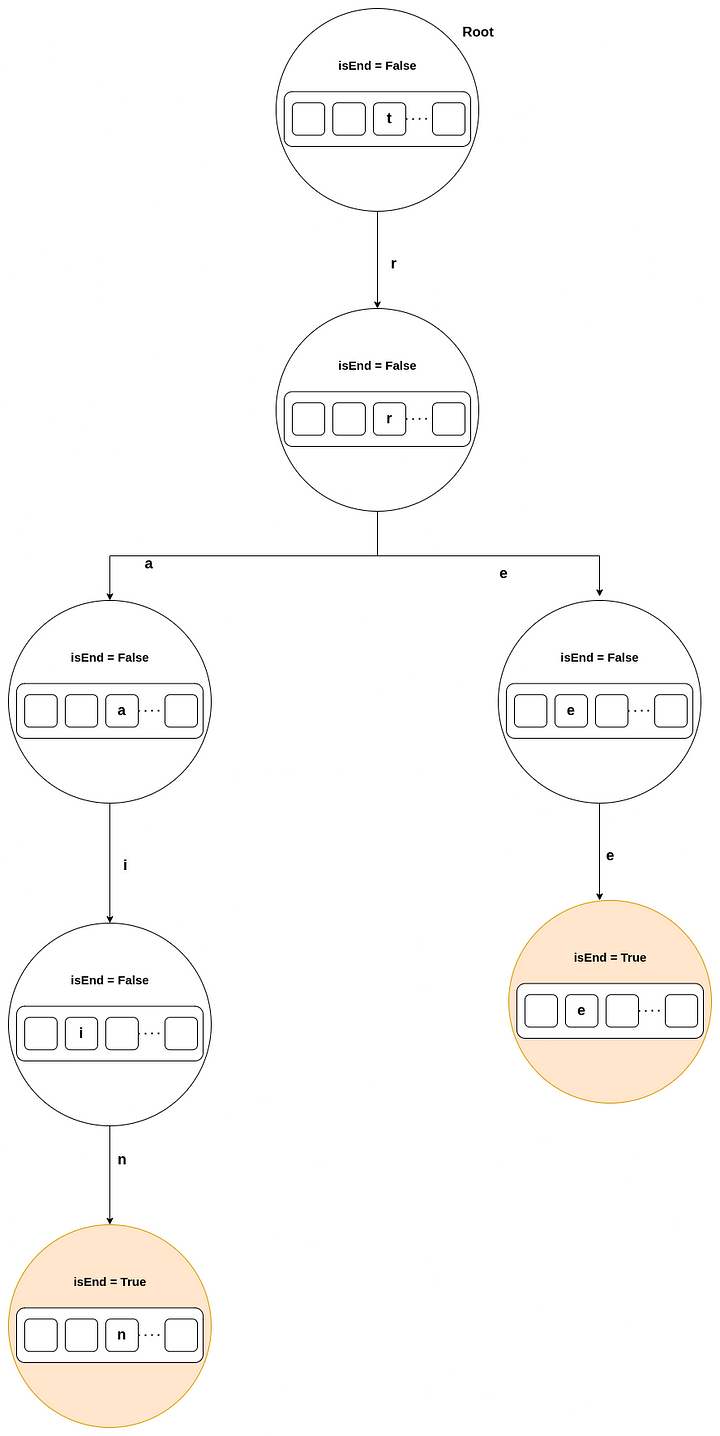
For example, the trie shown in the image below has two words, tree, and train. They have a common prefix, tr. The root of the trie represents an empty string. The nodes that are d edges away from the root represent the prefix of length d. The end of the word is marked with a different color. While coding, we will have a flag for each node which indicates if this node is an end of a word or not.

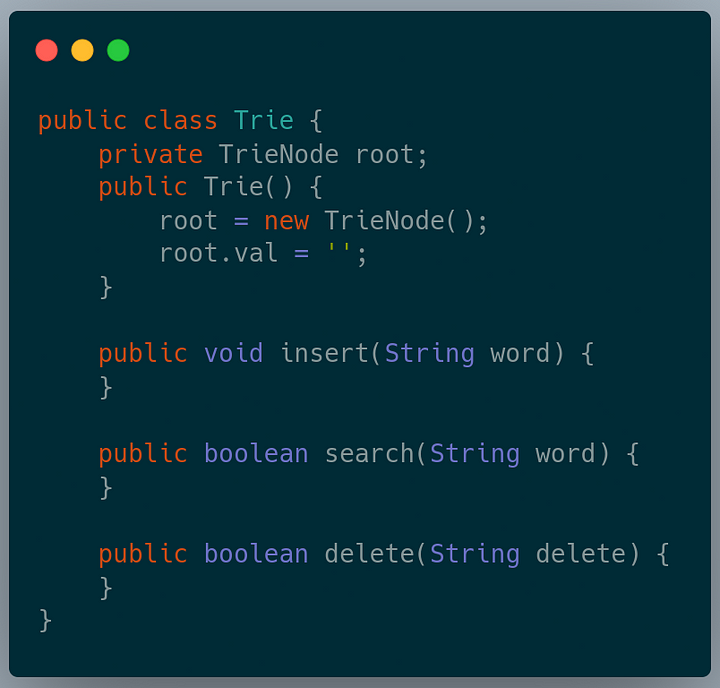
Following is the structure of the Trie class

Insertion in trie data structure

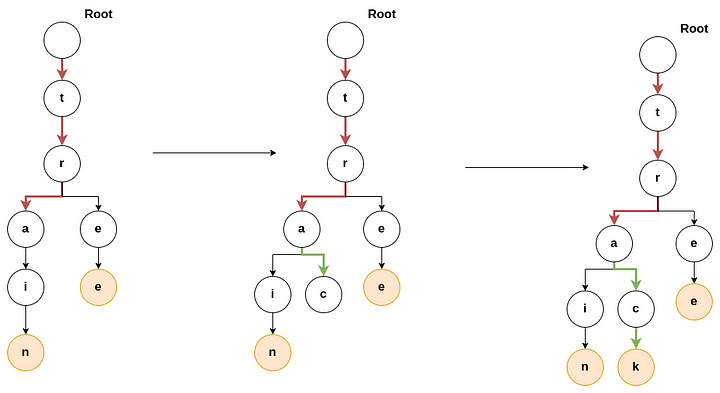
Now, we want to add the word track to the trie. We will start traversing the tree from the root. We will check if the root has a child node t or not. As the root has a child node t, We will move to that node. Now we will check if this node has a child node r or not. As this node has a child node r, we will move to that node. We will do this process until we reach the word’s end or if a node does not have the desired child node. Once we reach node a, three edges away from the root node, we see that this node does not have a child node c. So we insert a new node for character c in the trie, which is the child of the current node. Similarly, we do this for character k, as shown in the image. We mark node k as the end of the word track.

In the above image, the red arrows show the first part of insertion, where we traverse the nodes which are already present in the trie. The green arrows show the result after the addition of new nodes. 

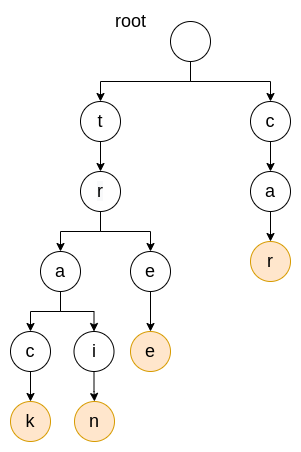
Similarly, the above image shows the result of adding the word car, which does not have any common prefix with the previously inserted words.

Steps for inserting a word in a trie

1. Start from the root node.
2. For each letter from left to right in the word, check if the current node has a child corresponding to that letter. 
3. If yes, go to that node.
4. If no, insert a new node as a child of the current node.
5. Repeat the above steps till you reach the end of the word.
6. Mark the end of the word flag as True for the last node.

Searching in trie data structure

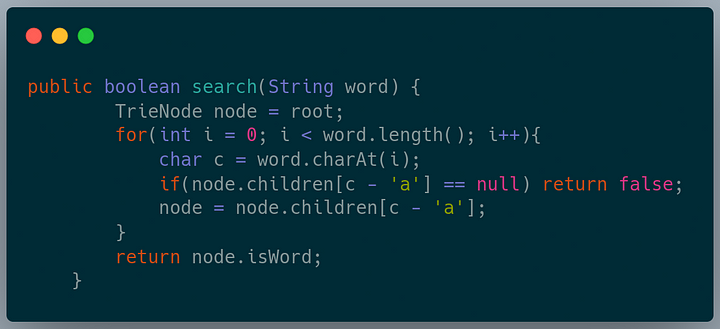
We want to find out if a word is present in the trie. Following are the steps for searching a word in a trie:

1. Start from the root node.
2. For each letter from left to right in the word, check if the current node has a child corresponding to that letter.
3. If no, return False(a word not found).
4. Repeat the above steps till you reach the end of the word.
5. Return True if the last node has the end of word flag set to True; else, return False.

Deletion in trie data structure

Delete a given word if it is present in the trie. For deleting a word in a trie, we search for that word in the trie. If we find the word in the trie, we set the end of the word flag of the last node to False.

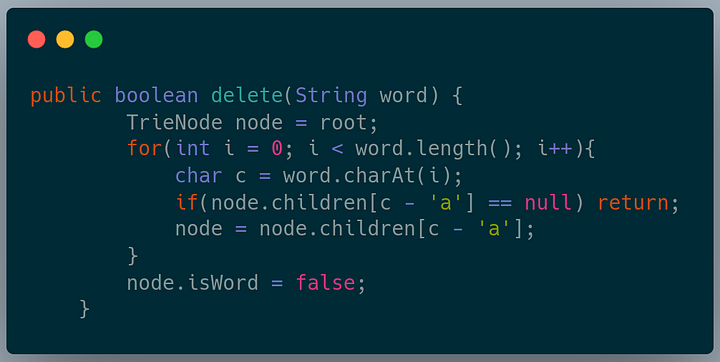
The time complexity of trie operations

For searching, inserting, and deleting some string s of length n in a trie, we need to follow at most n number of pointers from the root to the node for string s, if it exists. Each pointer can be looked up in O(1) time. So overall time complexity = n * O(1) = O(n), which is only dependent on the length of the string and independent of the number of strings in the trie!

The space complexity of trie operations

The space complexity of the trie depends on the number of nodes present in the trie. A trie with N nodes will need O(N*k) space due to the pointers in each node, where k is the total number of unique characters in the alphabet.

Applications of trie data structure

As we have studied till now, we can conclude that tries are very useful when working with prefixes; the words with the same prefixes share nodes and edges in the trie. Following are the questions that can be easily answered due to this property of tries:

1. Are there any words in the trie that start with a given prefix?
2. Find all words in the trie that start with a given prefix?

These properties are beneficial in the following real-life applications.

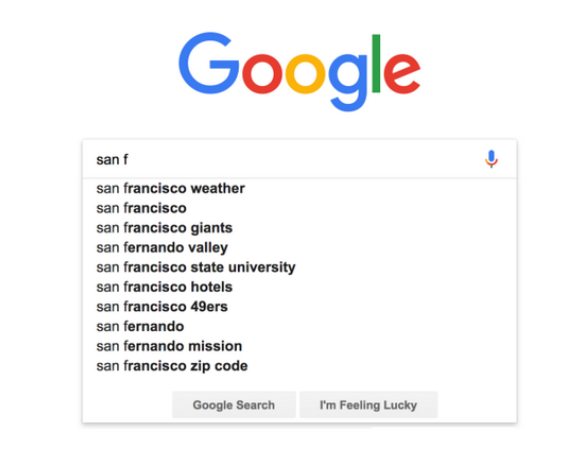
Autocomplete Feature in a search engine

We can store all the frequently used words in a trie. When a user starts typing their query, based on the prefix entered till now, we can suggest the words from the trie which have the same prefix. If the word that the user enters is not present in our trie, we can add that word to our trie to improve suggestions in the future. Following are some examples where autocomplete is used:

Longest prefix matching for IP Routing

The longest prefix match is an algorithm to lookup the IP prefix, the destination of the next hop from the router. Each router stores the IP prefix and the corresponding router in the routing table. We use this algorithm to find the prefix matching the given IP address and return the corresponding router node.

Consider the following example:

When we receive the IP address 192.168.20.19, node A should be chosen by the longest prefix matching algorithm.

The bold part of A and B’s IP is the prefix matching the given IP.

Using a brute force approach to find the node with the longest prefix common to the received IP is slow. It takes O(n * l) time, where n is the number of nodes and l is the length of the IP. We can see that as the number of nodes increases, the time taken increases linearly.

We can store the IP address of the nodes in the routing table in a trie and search for the node with the longest prefix. This approach will take O(l) time irrespective of the number of nodes in the routing table.

Example

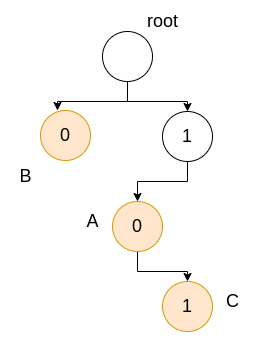
We have nodes A, B, and C in the routing table with the corresponding prefix of their IPs. Note that we only care about the unique prefixes, and we do not need to look at the entire IP address. Suppose the IP address we receive is *1011**. We need to look at the prefix of the input IP of length equal to the max length of the prefix stored in the routing table. We traverse the trie as shown below:

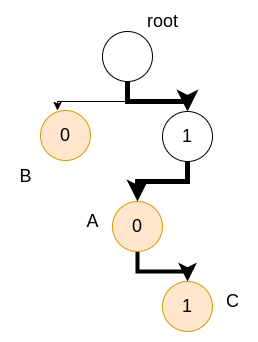
We can see that the node with the longest common prefix is C. The node chosen is C.

Spell Checker

This application is very similar to autocomplete. If the word entered by the user is not present in the trie, we suggest words with a common prefix to the word entered by the user.

Solving problems with trie

• Implement Trie (Prefix Tree)
• Longest Word in Dictionary
• Map Sum Pairs
• Word Search II
• Replace Words
• Add and Search Word — Data structure design
• Maximum XOR of Two Numbers in an Array

Enjoy learning, Enjoy algorithms!