Minimum Coin Change Problem

Difficulty: Medium, Asked-in: Microsoft, Amazon, Morgan Stanley

Key takeaway: An excellent optimization problem to learn problem-solving using dynamic programming.

Let’s understand the problem

We are given amount K representing total amount of money and integer array coin[] of size m representing coins of different denominations. Write a program to find the minimum number of coins required to make change.

We may assume that we have an infinite supply of each kind of coin with the value coin[0] to coin[m-1]. If any combination of the coins cannot make up amount K of money, we return -1.

Example 1

Input: coin[] = [25, 10, 5], K = 30, Output: 2

Explanation: Minimum 2 coins required: we can use one coin of 25 and one coin of 5.

Example 2

Input: coin[] = [9, 6, 5, 1], K = 13, Output: 3

Explanation: Minimum 3 coins required: we can use two coins of 6 and one coin of 1.

Example 3

Input: coin[] = [1, 3, 5, 7], K = 18, Output: 4

Explanation: Minimum 4 coins required. We can use any one of these combinations to provide change using 4 coins: (7, 7, 3, 1),(5, 5, 5, 3), and (7, 5, 5, 1).

Discussed solution approaches

• Brute force approach  using recursion
• Efficient approach  using bottom-up approach of dynamic programming

Brute force approach  using recursion

Solution idea and steps

This is an optimization problem because there can be several ways to provide change, but we need to return the change using the minimum number of coins. In other words, the solution space is huge, and only a few solutions will provide the optimal solution. So one basic idea would be to explore all solutions or possibilities of the change and return the count with a minimum number of coins. The critical question is: How do we implement this? Let’s think!

• In such a situation, when we need to explore all possibilities, we can think about solving the problem recursively, i.e., the solution of the problem using smaller sub-problems.
• Initially, available choices are important for building the recursive solution. Here we have m choices of coins at the start, i.e., we can pick any coin among m coins.
• Suppose minCoinChange(coin[], m, K) returns the minimum number of coins required to make the change of value K (This is our larger problem). If we select any coin[i] first, the smaller sub-problem is minCoinChange(coin[], m, K - coin[i]), i.e., the minimum number of coins required to make a change of amount K - coin[i].
• So, for i = 0 to m - 1, whichever choice provides the change using a minimum number of coins, we shall add 1 and return the value. Before selecting any coin, make sure whether the value of the coin is less than or equal to the amount needed, i.e., coin[i] <= K.

Recursive structure:

minCoinChange(coin[], m, K) = min (for i = 0 to m - 1) { 1 + minCoinChange(coin[], m, K - coin[i]) }

Where coin[i] <= K.

Base case: If K == 0, then 0 coins are required.

Solution code C++

int minCoinChange(int coin[], int m, int K)
{
    if (K == 0)
        return 0;
    int minCount = INT_MAX;
    for (int i = 0; i < m; i = i + 1)
    {
        if (coin[i] <= K)
        {
            int currCount = minCoinChange(coin, m, K - coin[i]);
            if (currCount != INT_MAX && currCount + 1 < minCount)
                minCount = currCount + 1;
        }
    }
    if (minCount == INT_MAX)
        return -1;
    else
        return minCount;
}

Solution code Python

def minCoinChange(coin, m, K):
    if K == 0:
        return 0
    minCount = -sys.maxsize
    for i in range(m):
        if coin[i] <= K:
            currCount = minCoinChange(coin, m, K - coin[i])
            if currCount != -sys.maxsize and currCount + 1 < minCount:
                minCount = currCount + 1
    if minCount == -sys.maxsize:
        return -1
    else:
        return minCount

Time and space complexity analysis

From the above observation, we can conclude that the total number of recursive calls will increase if we increase the value of K or m. Therefore, the time complexity depends on both K and m, where the input size is (K, m).

For the upper bound of worst-case analysis, let us assume that coin[i] <= K during each recursive call. Then, the recursion tree would be a full tree where each child has m nodes. So we have m number of recursive calls at the 1st level of the recursion tree, m^2 number of recursive calls at the 2nd level of the recursion tree, and so on.

The total number of recursive calls in the worst-case scenario is 1 + m + m^2 + ... + m^k = (m^(k+1) - 1) / (m - 1) = O(m^k), which is an exponential time. Note that the sum of the geometric progression S = a + ar + ar^2 + ... + ar^n = a(r^(n+1) - 1)/(r - 1), where r > 1.

In retrospect, this is not surprising because we are exploring all possibilities to provide change. If we create a recursion tree for the above approach, we can clearly notice overlapping or repeated subproblems.

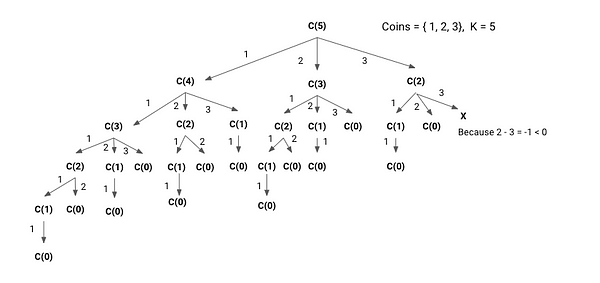
For example, the following picture shows the recursion tree diagram for K = 5 and coins of given values [1, 2, 3]. The sub-problem of size 3 appears 2 times, the sub-problem of size 2 appears 4 times, and the sub-problem of size 1 appears 7 times.

Efficient approach  using bottom-up approach of dynamic programming

Solution idea and steps

Since we have identified that it is a dynamic programming problem, we can solve it using the bottom-up approach. Our aim here is to calculate the solution to smaller problems in an iterative way and store their results in a table. The critical question is: How do we build the solution in a bottom-up manner? Let’s think!

1. Table structure: The state of the smaller sub-problems depends on the variable K because it decreases after each recursive call. Therefore, we need to construct a 1-D table to store the solutions of the sub-problems.
2. Table size: The size of the 1-D table is equal to the number of different subproblems. According to the recursion tree, there can be a total of (K + 1) different sub-problems, i.e., sub-problems of size (K, K-1, ..., 2, 1, 0). So we use the table of size k + 1 to store solutions of the subproblems i.e. Change[K + 1].
3. Table initialization: Before building the solution using an iterative structure of the bottom-up approach, we need to initialize the table with the base case, which is Change[0] = 0.
4. Iterative structure to fill the table: Now, we need to define an iterative structure to fill the table Change[i], i.e., a relation by which we build the solution of larger problems using the solutions of smaller problems in a bottom-up manner. We can easily define an iterative structure by using the recursive structure of the recursive solution. Change[i] = min (for j = 0 to m-1) { 1 + Change[i - coin[j]] }, where coin[j] <= i.
5. Returning the final solution: After filling the table iteratively, our final solution is stored at the last index of the array, i.e., we return Change[K].

Solution code C++

int miniCoinChange(int coin[], int m, int K)
{
    if (K == 0)
        return 0;
    int Change[K + 1];
    Change[0] = 0;
    
    for (int i = 1; i <= K; i = i + 1)
        Change[i] = INT_MAX;

    for (int i = 1; i <= K; i = i + 1)
    {
        for (int j = 0; j < m; j = j + 1)
        {
            if (coin[j] <= i)
            {
                int currCount = Change[i - coin[j]];
                if (currCount != INT_MAX && currCount + 1 < Change[i])
                    Change[i] = currCount + 1;
            }
        }
    }
    
    if (Change[K] == INT_MAX)
        return -1;
    else
        return Change[K];
}

Solution code Python

def minCoinChange(coin, m, K):
    if K == 0:
        return 0
    Change = [-sys.maxsize] * (K + 1)
    Change[0] = 0
    
    for i in range(1, K + 1):
        for j in range(m):
            if coin[j] <= i:
                currCount = Change[i - coin[j]]
                if currCount != -sys.maxsize and currCount + 1 < Change[i]:
                    Change[i] = currCount + 1
    
    if Change[K] == -sys.maxsize:
        return -1
    else:
        return Change[K]

Time and space complexity analysis

There are two nested loops in the code. The first loop iterates from 1 to K, and the second loop iterates from 0 to m-1. The time complexity is O(K*m), and the space complexity is O(K) for the extra array Change[] of size K + 1.

Critical ideas to think!

• Do we require the entire array of size K, or can we optimize the space? Think about the case when the amount is too high.
• How can we modify the code to find the coins that are part of the optimal solution?
• Can we solve this problem using some other approach? Can we think of applying the greedy or divide-and-conquer strategy?
• Explore DP problems that can be solved using a similar idea.
• Why is the recursive solution exponential time? Try analyzing the recursive code using the recursion tree method.
• Consider the top-down approach to solving this problem.

Suggested problems to solve

• Find the number of ways in which you can change an amount with given coins of different denominations.
• Greedy algorithm to find the minimum coin count.
• Rod cutting problem
• 0–1 Knapsack problem
• Weighted job scheduling

If you have any queries/doubts/feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!