Types of Graph in Data Structures

The first step in any graph problem is understanding the types of graphs you are dealing with. This would help us to extract various specific properties to solve and model the graph problem efficiently. Let’s discuss some of the popular types of graph in data structures.

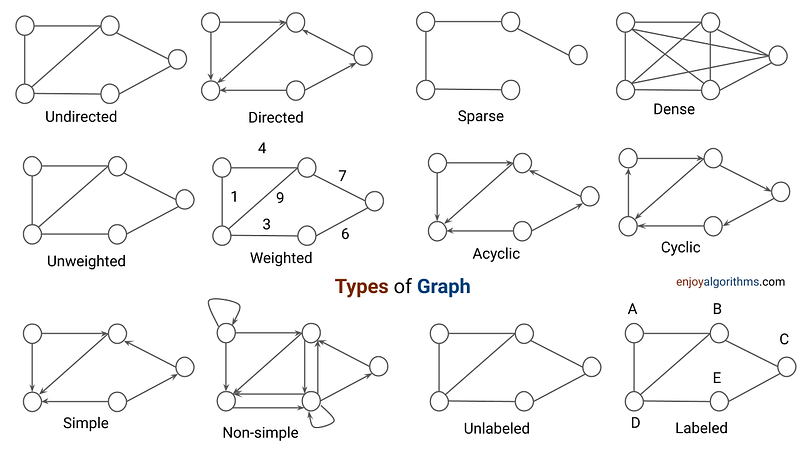
Undirected and Directed Graph

In an undirected graph, edges between vertices do not have a specific direction, and we can traverse from one vertex to another in both directions. For example, if there is an edge between vertex A and vertex B, it implies that we can travel from A to B as well as from B to A.

A good real-life example of an undirected graph is a social network. We can represent each user as a vertex and connections or friendships between users as edges. Since friendships are bidirectional (if user A is friends with user B, then user B is also friends with user A), an undirected graph is an appropriate representation.

In a directed graph, we can only traverse from one vertex to another in a specific direction determined by the edge. For example, if there is an edge between vertex A and vertex B, we can only travel from A to B.

A real-life example of a directed graph is a road network with one-way streets. In many cities, road systems are designed with streets that have specific directions of travel. Each intersection in the road network can be represented as a vertex, and the roads between intersections are represented as directed edges. The direction of the edge indicates the allowable movement of vehicles from one intersection to another.

Directed graphs are commonly used to model relationships or dependencies where the direction of interaction matters. For example, directed graphs can represent processes, flows, networks, or any scenario where there is a clear relationship or a specific order of events.

Weighted and Unweighted Graph

In an unweighted graph, edges between vertices do not have any associated numerical values or weights. Here, all edges are considered equal and have the same cost. In other words, the connections between vertices indicate only the presence or absence of a connection.

Unweighted graphs are used when the focus is on studying the structural properties of a graph or analyzing the connectivity between vertices, rather than considering varying costs or distances associated with edges.

A weighted graph is a type of graph in which each edge is assigned a numerical value or weight. These weights can represent various factors depending on the application. For example, in a road network graph, the weights of the edges could represent the length of the road, the travel time required to traverse the road, or the speed limit on that road. In other contexts, the weights could represent costs, capacities, probabilities, or any other relevant metric.

The weights in a weighted graph can be positive, zero, or even negative, depending on the specific problem and the semantics associated with the weights. So, the presence of weights in a graph affects various graph algorithms, particularly those focused on finding optimal paths or minimizing costs.

Sparse and Dense Graph

In an undirected graph with N vertices, the maximum possible number of edges that can exist is N * (N — 1) / 2, assuming there are no self-loops or parallel edges. Based on the number of edges in comparison to the number of vertices, we classify the graph as either dense or sparse.

In a sparse graph, the number of edges is significantly smaller compared to the maximum number of possible edges. In other words, there are relatively few edges in relation to the number of vertices. In a dense graph, the number of edges is close to the maximum possible number of edges. In other words, there is a significant number of edges in relation to the number of vertices.

• There is no official boundary between what is called sparse and what is called dense, but typically dense graphs have a quadratic number of edges, while sparse graphs are linear in size. In other words, the sparsity of a graph is a relative concept and can vary depending on the specific context and the given problem. A graph that may be considered sparse in one scenario may be considered dense in another!
• The sparsity of a graph can be described in terms of its edge density. Edge density is defined as the ratio of the number of edges in the graph to the maximum number of possible edges. In a sparse graph, the edge density is relatively low.

We can observe the sparse nature of a graph in several applications where connections between vertices are limited. For example, in social networks, not everyone is connected to every other person, resulting in a sparse graph representation. Similarly, road networks must be sparse graphs because any intersection can be the endpoint of only a few roads.

The density of a graph affects the choice of graph representation. For example, we use an adjacency list to represent sparse graphs and adjacency matrices to represent dense graphs. On the other hand, graph density can have implications for various graph algorithms. For example, algorithms that rely on dense connectivity may be more suitable for dense graphs. However, algorithms designed to handle sparse graphs may not be as efficient in dense graphs due to the increased computational and memory requirements.

Cyclic and Acyclic Graph

A cycle in a graph is a path that starts and ends at the same vertex, traversing one or more edges. So acyclic graph contains at least one cycle. In other words, a cyclic graph has a sequence of edges that can be followed to return to a vertex, forming a closed loop.

On the other hand, a graph that does not contain any cycles is called an acyclic graph or a forest (if it consists of multiple disconnected components). In an acyclic graph, it is not possible to traverse a path and return to the starting vertex without revisiting any other vertices.

Cycles in graphs can have implications for various graph algorithms. Here are some examples:

• The Dijkstra algorithm for finding the shortest path will not work when there is a negative cycle in the path from the source to the destination. In simple terms, we cannot define the shortest path in a graph with the existence of a negative cycle. Similarly, if there is a cycle with positive weight, we cannot define the longest path in the graph.
• If the graph is a directed acyclic graph (DAG), we can topologically sort the graph vertices based on the order of edges, where every directed edge goes in one direction from the first vertex to the last vertex in a topologically sorted order. For example, an edge (u, v) indicates that node u must occur before v. On the other hand, we cannot perform topological sorting in cyclic graphs.
• Checking the presence of a cycle is a critical step in several graph problems. For example, in the case of a DAG, topological sorting is typically the first step in any algorithm. This can help us design several algorithms efficiently, such as finding the shortest path or finding the longest path in a DAG.

Note: We will write a separate blog on cyclic graphs, directed acyclic graphs, and topological sorting.

Connected and Disconnected Graph

In a connected graph, there is a path between every pair of vertices. In other words, for any two vertices in a connected graph, there exists a sequence of edges to travel from one vertex to the other.

• Every vertex is reachable from any other vertex in a connected graph. So there are no isolated vertices or disconnected components within the connected graph. 
• The concept of connectedness is important in graph. For example, when working with connected graphs, we can find the shortest path between any pair of vertices or determine the minimum spanning tree.

A graph that is not connected is called a disconnected graph. In other words, a graph is considered disconnected if there exist two vertices, u and v, in the graph such that there is no path from u to v. So such graph can be divided into two or more separate connected components, where all vertices within a component are connected to each other, but there are no edges that connect vertices across different components.

• Disconnected graphs can occur in various scenarios where there are isolated subsets or clusters of vertices that have no connection to the rest of the graph. For example, in a social network graph, a disconnected graph might indicate separate groups of people who have no connections or interactions with each other.
• The presence of disconnected components in a graph can affect various graph algorithms. For example, algorithms that rely on graph traversal or connectivity, such as finding the shortest path or determining the minimum spanning tree, may need to be modified or applied separately to each connected component.
• In the case of disconnected graphs, we focus on the properties and characteristics of each connected component individually. The number and sizes of the connected components provide insights into the structure and connectivity of the graph.

In the coming future, we will add more insights to this blog. We hope you enjoyed the blog. Enjoy learning, enjoy algorithms!